نظریه ی بازی ها – قسمت دوم / آرنوش گلستانیان

بررسی و حل معمای زندانی:

دو نفر متهم به شرکت در یک سرقت مسلحانه، در جریان یک درگیری دستگیر شده‌اند و هر دو جداگانه مورد بازجویی قرار می‌گیرند. در طی این بازجویی با هریک از آن‌ها جداگانه به این صورت معامله می‌شود:                اگر دوستت را لو بدهی تو آزاد می‌شوی ولی او به پنج سال حبس محکوم خواهد شد.
اگر هر دو یکدیگر را لو بدهید، هر دو به سه سال حبس محکوم خواهید شد.
اگر هیچ‌کدام همدیگر را لو ندهید، هر دو یک‌سال در یک مرکز بازپروری خدمت خواهید کرد.
در این بازی به نفع هر دو زندانی است که هر دو گزینه سوم را انتخاب کنند، ولی چون هر کدام از آن‌ها به دنبال کسب بهترین نتیجه برای خود یعنی آزاد شدن هستند و به طرف مقابل نیز اعتماد ندارند و دوست خود را لو می‌دهند و در نتیجه هر دوی زندانی‌ها متضرر می‌شوند.

نتیجه­ی تصمیم گیری هر زندانی را در جدول زیرکه به ماتریس سود معروف است، نشان می­دهیم. برای مثال اگر بازیگر اول به گنهکار بودن دوست خود اعتراف کند ولی بازیگر دوم سکوت اختیار کند، بازیگر اول آزاد می­شود ولی دوست او به 5 سال حبس محکوم می­گردد و این نتیجه را در خانه­ی پایین و سمت چپ جدول نشان می­دهیم. همچنین نام بازیگران در بالا و سمت چپ جدول نوشته می­شود که مشخص شود هر عمل مربوط به کدام بازیگر است.

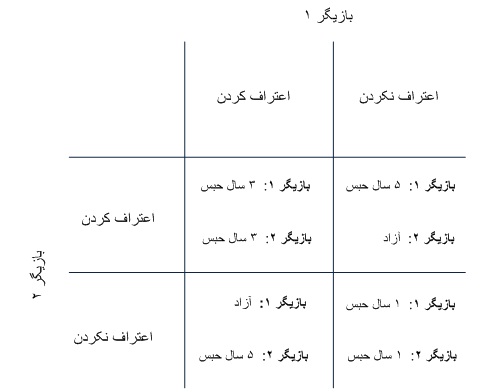
می­خواهیم تصمیم هر بازیگر را بررسی کنیم. باید توجه کنیم که هر بازیگر تصمیمی را اتخاذ می­نماید که بیشترین سود را برای وی داشته باشد که در اینجا کمتر بودن میزان حبس است. می­دانیم که هر بازیگر از تصمیمات فرد دیگر اطلاعی ندارد. ابتدا بهترین تصمیمی که بازیگر دوم اتخاذ می­نماید را بررسی می­نماییم. وی ابتدا فرض می­کند که دوستش( بازیگر اول) به گناهکار بودن او اعتراف می­کند. در این حالت او بین 3سال حبس و 5 سال حبس (ستون سمت چپ)، 3 سال حبس را انتخاب می­کند و اعتراف می­کند. در مرحله­ی دوم او فرض می­کند که بازیگر اول سکوت اختیار کند. بنابراین او بین 1سال حبس و آزادی ( ستون سمت راست) آزادی را انتخاب می­نماید و اعتراف می­کند. پس به طور کلی بازیگر دوم مستقل از تصمیم بازیگر اول ترجیح می­دهد که اعتراف کند.

بازیگر اول نیز به همین نحو تصمیم گیری می­نماید. ابتدا فرض می­کند بازیگر دوم به گناهکار بودن او اعتراف نماید در این صورت بهترین تصمیمی که او می­تواند اتخاذ نماید اعتراف کردن است که مجازاتش 3 سال حبس است و اگر فرض کند که دوست وی سکوت اختیار کرده است، او تصمیم به اعتراف کردن می­کند که پاداش آن آزادی است.

   تا به اینجا بررسی کردیم که هر بازیگر مستقل از انتخاب بازیگر دیگر، تصمیم به اعتراف کردن می­کنند و مجازات هر دو( خانه ی بالا و سمت چپ) 3 سال زندان است. ولی این دو بازیگر می­توانستند تصمیم بهتری بگیرند و فقط به 1 سال زندان بروند ولی چون هرکدام درصدد بیشتر کردن سود خود بودند بهترین انتخاب را از دست دادند.

می­توان معمای زندانی را به بسیاری از مسائل اجتماعی دیگر تعمیم داد به شرطی که بتوان افراد جامعه را به دو دسته تقسیم کرد و قوانینی نظیر آنچه گفته شد، تعیین کرد. برای مثال رقابت دو شرکت بر سر تعیین قیمت یک کالای مشابه همانند مثال بحث شده حل می­شود. در ادامه مثال ساده دیگری از نظریه بازی­ها را به همراه ماتریس سود آن بیان می­کنیم.

بازی باخ یا استراوینسکی( Battle Of sexes )

مثال معروف دیگری از نظریه بازی­ها مثال باخ یا استراوینسکی ( دو آهنگساز معروف) است. شرح این مثال به صورت زیر است.

در یک خانواده دو نفره زن و شوهری می­خواهند به کنسرت بروند و آهنگساز دلخواه خانم و آقا متفاوت است. آهنگساز مورد علاقه­ی خانم استراوینسکیاست در حالیکه آقا ترجیح می­دهد به کنسرت باخ برود. همچنین باید در نظر گرفت که هر دو فرد ترجیح می­دهند با هم به یک کنسرت بروند. میزان خوشحالی یا احساس رضایت هرکس را با عدد در ماتریس سود زیر نشان می­دهیم.

با استدلالی همانند مثال قبل این نتیجه بدست می­آید که این دو بازیگر تصمیم می­گیرند به یک کنسرت بروند و نوع آن مهم نیست. مشاهده می­کنید که در این مثال با توجه به متفاوت بودن ماتریس­ سود نسبت به معمای زندانی، بازیگران به گونه­ای دیگر تصمیم­گیری می­نمایند زیرا هدفشان یافتن بهترین تصمیم با درنظرگیری شرایط موجود است. در مثال قبل فقط یک نقطه برای هر دو بازیگر مطلوب بود. به عبارت دیگر، بازیگران فقط در یک نقطه انگیزه­ای برای تغییر بازینداشتند و اصطلاحا فقط یک تعادل نش موجود بود. در حالیکه در این مثال دو تعادل نش موجود است. در قسمت بعدی درباره­ی تعادل نش و تعریف آن بیشتر توضیح می­دهیم.

منابع:                            

• نظریه بازیها و کاربردهای آن: بازیهای ایستا و پویا با اطلاعات کامل، قهرمان عبدلی، سازمان انتشارات جهاد دانشگاهی واحد تهران، ۱۳۸۶
• مقاله درس نظریه الگوریتمی بازی­ها، کاربردهاينظريهبازيدرمسائلشبکه­هايبي­سيم، مسعود فریور، 1387
• نظریه بازی­ها “استرتژی رقابتی”، بیژن توسلی حضوری، انتشارات صنعت فولاد، 1371